https://www.acmicpc.net/problem/1238

문제 분석
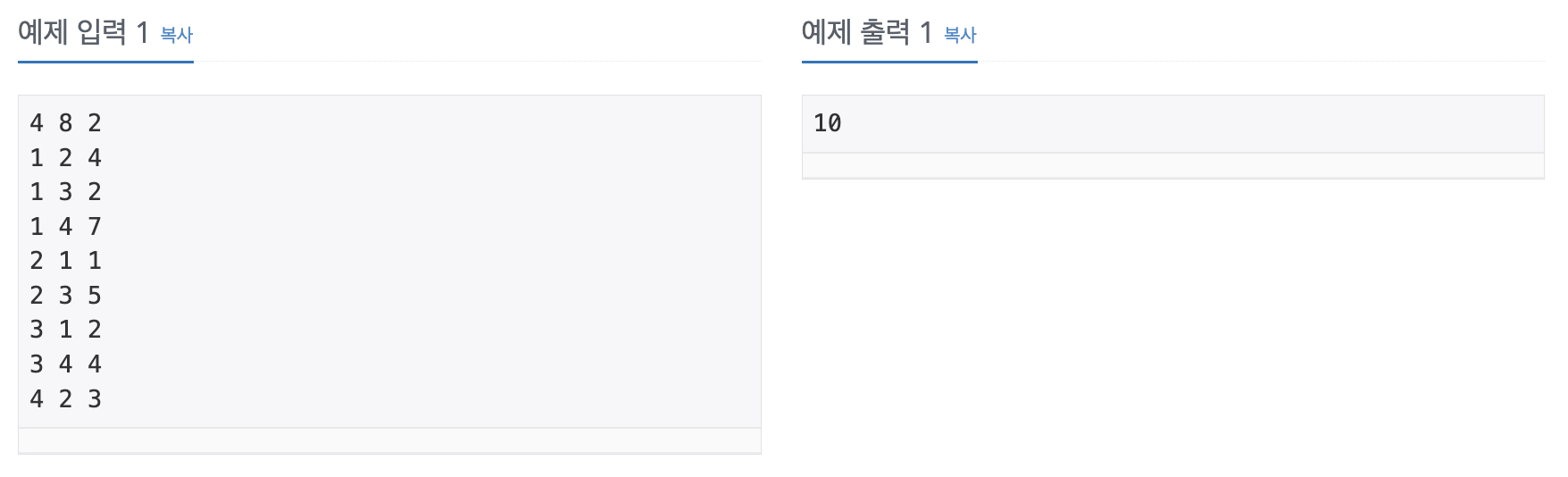
- N개의 숫자로 구분된 마을에 한 명의 학생이 살고 있다.
- N명의 학생이 x (1 <= x <= n)번 마을에 모여서 파티를 벌이기로 했다.
- 이 마을 사이에는 총 M개의 단방향 도로들이 있고, i번째 길을 지나는데 Ti (1 <= Ti <=100) 시간을 소비한다.
- 각 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다. - 최단거리
- 오고가는 길이 다를 수 있다.
- N명의 학생들 중 오고 가는데 가장 많은 시간을 소비하는 학생은 누구인가
풀이
- N명의 학생
- M 개의 이동할 수 있는 도로 정보 (단방향, 가중치)
- X : 모이는 곳
- 1 ~ N 까지 반복
- distance[ i ] = i ~ X 의 최단거리 + X ~ i 의 최단거리
- 이 중 가장 큰 값을 출력
코드 설계
- X에서 1~N까지의 최단거리는 다익스트라로 한번에 구하기
- 1 ~ N까지 방문하면서 시작 노드 설정
- 1에서 X까지의 최단 거리 : 다익스트라
- 가중치가 있는 시작 - 도착점에 대한 최단거리
- 시작점과 연결된 점들 찾기
- 도착 지점에 대해서만 거리 저장(int(1e9))? or 다 저장하고 도착지점에 대해서만 return
- 현재 노드에서의 이동이 이전의 이동거리보다 짧다면 update
- x위치에 대한
정답 코드
실패
import sys, heapq
input = sys.stdin.readline
N, M, X = map(int, input().split())
g = [[] for _ in range(N+1)]
for _ in range(M) :
u,v,w = map(int, input().split())
g[u].append((v, w)) # next_node, 거리
INF = int(1e9)
# 각 마을에서 X에 도착하는 최단거리
distance_go = [INF for _ in range(N+1)]
min_dis = [0 for _ in range(N+1)]
def dijkstra(s_node) :
distance = [INF for _ in range(N + 1)] # N은 1부터 N까지
hq = []
heapq.heappush(hq, (0, s_node))
while hq :
dis, now_node = heapq.heappop(hq)
# 현재 노드와 연결된 것들
for i in range(len(g[now_node])) :
next_node = g[now_node][i][0]
if g[now_node][i][1] + dis < distance[next_node] :
distance[next_node] = g[now_node][i][1] + dis
heapq.heappush(hq, (distance[next_node], next_node))
# X에서 (1~N) 각 마을로 돌아오는 최단거리
dijkstra(X)
for i in range(1, N+1) :
min_back =
# 1~N 마을에서 X까지의 최단거리
for i in range(1, N+1) :
dijkstra(i) # 시작 마을 지정
if i==X :
min_dis[i] = 0
continue
min_dis[i] = distance[X]
ans = []
for i in range(1, N+1) :
ans.append(distance_go[i] + min_dis[i])
print(max(ans))
다른 정답 코드 1 : gpt
import sys, heapq
input = sys.stdin.readline
N, M, X = map(int, input().split())
g = [[] for _ in range(N+1)]
reverse_g = [[] for _ in range(N+1)] # 역방향 그래프
for _ in range(M) :
u,v,w = map(int, input().split())
g[u].append((v, w)) # next_node, 거리
reverse_g[v].append((u,w)) # X에서 마을로 가는 거리 계산
INF = int(1e9)
def dijkstra(s_node, g) :
distance = [INF for _ in range(N + 1)] # N은 1부터 N까지
distance[s_node] = 0
hq = []
heapq.heappush(hq, (0, s_node))
while hq :
dist, now = heapq.heappop(hq)
# 현재 노드의 이동거리가 현재까지 계산한 최소 거리보다 크다면 pass
# 최소를 만들 수 없음
if dist > distance[now] :
continue
# 현재 노드와 연결된 것들
for next_node, cost in g[now] :
new_dist = dist + cost
if new_dist < distance[next_node] :
distance[next_node] = new_dist
heapq.heappush(hq, (new_dist, next_node))
return distance
dist_from_X = dijkstra(X, g)
dist_to_X = dijkstra(X, reverse_g)
max_time = 0
for i in range(1, N+1) :
max_time = max(max_time, dist_from_X[i] + dist_to_X[i])
print(max_time)
2회차 - 25.04.07
import sys, heapq
input = sys.stdin.readline
'''
N명의 학생이 X번 마을에 모여서 파티를 벌이기로 하였다.
M개의 단방향 도로, Ti 시간 소요
최단시간으로 갔다가 돌아오려고 한다.
가장 많은 시간이 걸리는 학생은?
왜 다익스트라를 선택하였는가 -> 방향이 있는 거리의 최단 거리를 구하는 문제
'''
INF = 1e9
N, M, X = map(int, input().split())
# M개의 도로에 대한 (시작 마을, 도착 마을, 소요시간/비용)
dp_ori = [[] for _ in range(N+1)] # 1~N번 마을 연결 정보
dp_rev = [[] for _ in range(N+1)]
for _ in range(M) :
start, end, cost = map(int, input().split())
dp_ori[start].append([end, cost])
dp_rev[end].append([start, cost])
def dijkstra(start_node, dp) :
'''
다익스트라란?
시작점에 대해 모든 노드에 대한 최단 거리 return
시작점과 연결된 값 확인
그 중 최단 거리 갱신
'''
dist = [INF for _ in range(N + 1)] # 최단거리를 저장하는 list
# dist_rev = [INF for _ in range(N+1)]
hq = []
heapq.heappush(hq, (0, start_node)) # (거리, 시작노드) : 시작 노드에 대한 거리는 0
dist[start_node] = 0
# dist_rev[start_node] = 0
while hq : # 모든 경로에 대해 확인 - 갱신 or not
now_dist, node = heapq.heappop(hq)
# 현재 노드와 연결된 도로의 수만큼 반복
for i in range(len(dp[node])) :
# 현재 노드와 연결된 노드까지의 경로에 대해 만약 현재 노드에서 이동하는게 더 적은 비용이 든다면 갱신
next_node = dp[node][i][0]
distance = dp[node][i][1]
if dist[node] + distance < dist[next_node] :
dist[next_node] = dist[node] + distance
heapq.heappush(hq, (dist[next_node], next_node))
#
# if dist_rev[node] + distance < dist_rev[next_node] :
# dist_rev[next_node] = dist_rev[node] + distance
return dist
from_x = dijkstra(X, dp_ori) # X 마을에서 각 마을로 돌아가는 최단 거리
to_x = dijkstra(X, dp_rev) # 각 마을에서 X로 가는 최단거리
max_dist = -INF
for i in range(1, N+1) : # 1번 마을부터 N번 마을까지
if from_x[i] == INF or to_x[i] == INF :
continue
sum_dist = from_x[i] + to_x[i]
max_dist = max(max_dist, sum_dist)
print(max_dist)'코딩 테스트 > 백준' 카테고리의 다른 글
| [Python] 백준 16236 아기 상어 (0) | 2025.04.07 |
|---|---|
| [Python] 백준 2583 영역 구하기 (0) | 2025.04.04 |
| [Python] 백준 9095 1,2,3 더하기 (0) | 2025.04.02 |
| [Python] 백준 2217 로프 (0) | 2025.04.01 |
| [Python] 백준 2212 센서 (0) | 2025.03.27 |



