[알고리즘] 그래프 (Graph) - 1. 개념

코딩 테스트 합격자되기 chap 11 그래프를 바탕으로 작성하였습니다.

 

그래프의 개념

그래프는 노드(vertex)와 간선(edge)을 이용한 비선형 데이터 구조이다.
보통 그래프는 데이터간의 관계를 표현하는 데 사용

노드 : 데이터
간선 : 노드 간의 관계나 흐름 - 간선은 방향이 있을 수도 없을 수도 있다. + 가중치

📌 그래프 용어 정리

https://goldenrabbit.co.kr/wp-content/uploads/2023/12/%EC%8A%A4%ED%81%AC%EB%A6%B0%EC%83%B7-2023-12-11-%EC%98%A4%EC%A0%84-9.24.55.png

 

• 노드 : 동그라미로 표현한 것 → 데이터가 담겨있다.
• 간선 : 화살표
• 가중치 : 간선 위 숫자

 

📌 그래프의 종류와 특징

그래프는 방향성, 가중치, 순환 특성에 따라 종류를 구분할 수 있다.

1. 흐름을 표현하는 방향성

• 방향 그래프(directed graph) : 방향이 있는 간선을 포함한 그래프
• 무방향 그래프(undirected graph) : 방향이 없는 간선을 포함한 그래프

2. 흐름의 정도를 표현하는 가중치

• 가중치 그래프(weigth graph) : 데이터의 흐름의 방향 뿐만 아니라 양을 의미하는 가중치가 있는 그래프

3. 시작과 끝의 연결 여부를 보는 순환

• 순환 그래프(cycle graph) : 특정 노드에서 시작해 간선을 따라 다시 돌아오는 경로가 있는 (순환) 그래프
• 비순환 그래프(acyclic graph)

 

📌  그래프 구현

ex) 서울에서 부산으로 유동 인구가 8,000명 발생했다는 내용을 그래프로 표현한다면 -

• 데이터를 담고 있는 노드 : 서울, 부산
• 노드를 연결하고 있는 간선 : 서울과 부산의 연결 유무
• 간선의 방향 : 서울에서 부산 방향으로
• 간선의 가중치 : 유동 인구 8,000명

 

인접 행렬 그래프 표현

인접 행렬은 배열을 활용하여 구현할 수 있다.

• 배열의 index : 노드
• 배열의 값 : 노드의 가중치
• 인덱스의 세로 방향 : 출발 노드
• 인덱스의 가로 방향 : 도착 노드

이전의 서울에서 부산으로 향하는 간선이 있는 그래프와 인접 행렬은 다음과 같이 표현할 수 있다.

서울(0) → 부산(1)으로 향하는 가중치가 400(km)인 그래프가 표현

 

인접 리스트 그래프 표현

인접 리스트로 그래프를 표현하기 위해 다음과 같은 적절한 노드를 정의해야 한다.
이때 값(v)과 가중치(w), 다음 노드(next)를 묶어서 관리한다.

인접 리스트 그래프 표현 방식은 다음과 같은 과정으로 동작한다.

1. 노드의 개수만큼 배열 준비한다.
2. 배열의 인덱스는 각 시작노드를 의미하며 배열의 값에는 다음 노드를 연결한다.

 

동작 과정은 다음과 같다.

1단계 ) 노드의 개수만큼 배열 준비

 

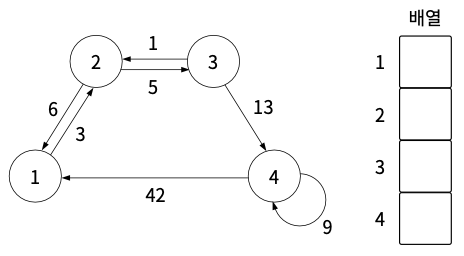
2단계 ) 1 → 2 (가중치 3)을 표현하면 다음과 같다.

출발 노드 : index = 1
도착 노드 : v = 2
가중치 : w = 3

 

3단계 ) 2→ 1 (가중치 6)을 표현하면 다음과 같다.
출발 노드 : index = 2
도착 노드 : v = 1
가중치 : w = 6

 

4단계 ) 정의한 노드의 다음 노드가 연결되는 모습은 다음과 같이 나타낼 수 있다.
2 → 3 (가중치 5)을 표현하면 다음과 같다.
이미 배열에는 노드 2가 연결되어 있다.
다음 노드가 Null 인 노드를 찾아 2 → 3 (가중치 5)을 표현한 노드를 연결한다.

 

5단계 ) 같은 방식으로 그래프를 연결하면 다음과 같이 인접 리스트를 완성할 수 있다.

 

✅ 인접 행렬과 인접 리스트의 장단점

인접 행렬의 장단점

단점 1 : 인접 행렬로 희소 그래프를 표현하는 경우

• 희소 그래프 : 노드 수에 비해 간선 수가 매우 적은 그래프
  
  
• 인접 행렬은 크기가 고정되어 있으므로 최악의 경우를 고려해서 크기를 결정
• 따라서 노드가 N개 있을 때 모든 간선이 연결되는 최악의 경우를 고려해서 N × N 크기의 인접 행렬이 필요
• 이럴 때 간선 수가 적으면 이렇게 확보한 N × N 크기의 인접 행렬 공간 중 대부분의 공간은 실제로 사용하지 않으므로 비효율적

단점 2 : 노드들의 값의 차이가 매우 큰 그래프를 표현하는 경우

• 예를 들어 노드값이 순차적으로 증가하지 않고 1, 2, 3, 999와 같이 간격이 크면
• 가장 큰 노드의 값인 999를 기준으로 인접 행렬의 크기를 잡아야 한다.

장점

• 간선의 정보를 확인할 때의 시간 복잡도가 O(1)로 좋다.
• 인접 행렬에서는 인덱스 임의 접근으로 노드 간 간선 정보를 바로 확인 가능하기 때문이다.
• 구현 난이도가 낮다.

 

인접 리스트의 장단점

• 인접 행렬과 정반대의 장단점
• 인접 리스트는 실제 연결된 노드에 대해서만 노드의 값을 노드에 담아 연결하기만 하면 된다.
• (물론 최악의 경우 각 노드에서 모든 노드에 간선이 연결되어 있을 때는 효율이 떨어질 수 있다.)
• (보통은) 인접 리스트를 활용하면 메모리를 아낄 수 있다.
• 간선 정보를 확인할 때 특정 노드에서 시작하여 연결된 노드 개수가 많을수록 노드를 연결한 리스트의 길이만큼 탐색
  → 탐색 시간 : O(N)

 

✅

 

 

 

 

reference

이미지 출처

https://goldenrabbit.co.kr/2023/12/11/%EC%BD%94%EB%94%A9-%ED%85%8C%EC%8A%A4%ED%8A%B8-%ED%95%A9%EA%B2%A9%EC%9E%90-%EB%90%98%EA%B8%B0-%EA%B7%B8%EB%9E%98%ED%94%84-1-%EA%B7%B8%EB%9E%98%ED%94%84%EC%9D%98-%EA%B0%9C%EB%85%90/