[Python] 프로그래머스 lv.2 조이스틱
https://school.programmers.co.kr/learn/courses/30/lessons/42860
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
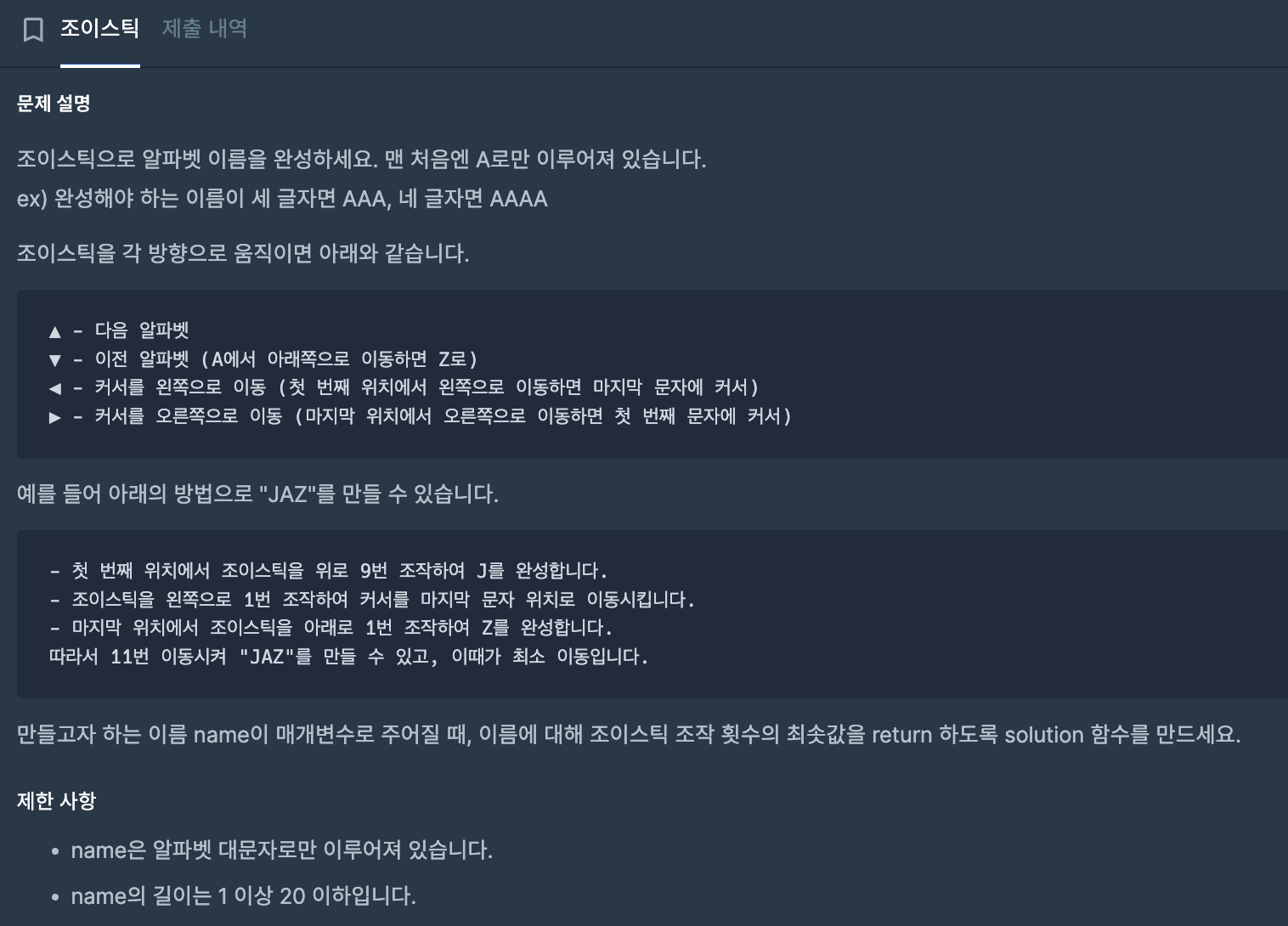

문제 분석
- 최소한으로 조이스틱을 움직여서 주어진 알파벳을 만들 때, 움직인 횟수 return
- 맨 처음에는 주어진 알파벳의 글자 수만큼 A로만 이루어져 있다.
코드 설계
- 수정이 필요한 글자의 idx 확인 (최단 이동거리를 위해)
- 이동 거리에 대한 최솟값
- 알파벳 수정에 대한 최솟값
정답 코드
실패
def solution(name):
ans = 0
init = list('A' * len(name))
modi_idx = []
# 수정이 필요한 글자 위치 찾기
for i in range(len(name)) :
if init[i] != name[i] :
modi_idx.append(i)
be_idx = 0
for idx in modi_idx :
# 최소 글자 이동 고려 (v)
if idx-be_idx < (be_idx + len(name) - idx + 1) : # 정방향 vs. 역방향
ans += abs(idx-be_idx)
else :
ans += (be_idx + len(name) + 1) - idx
# 최소 수정 횟수 / 목표 알파벳 : name[idx]
if ord(name[idx]) - ord('A') < ord('Z') - ord(name[idx]) + 1 :
ans += abs(ord(name[idx]) - ord('A'))
else :
ans += ord('Z') - ord(name[idx]) + 1
init[idx] = name[idx]
be_idx = id
return ans
- 연속되는 A가 있을 때, 그것의 왼쪽이나 오른쪽부터 시작하며 알파벳을 변경하는 것이 효율적이다.
- 이전처럼 다음 인덱스와 비교하면서 정방향과 역방향 만을 비교하면 모든 'A'가 연속된 경우 최적의 이동 경로를 보장하지 못할 가능성이 있다.
- 따라서 중간에 A가 있을 경우 우회하는 방법까지 고려
연속되는 A의 길이가 가장 긴 부분을 안가는 것이 효율적 - → 완전 탐색 (Brute Force)
def solution(name) :
ans = 0
# 기본 최소 좌우이동 횟수는 길이-1
min_move = len(name)-1
for i, char in enumerate(name) :
# 변경에 대한 최솟값
ans += min(ord(char)-ord('A'), ord('Z')-ord(char)+1)
# 해당 알파벳 다음부터 연속된 A 문자열 찾기
next = i+1
while next < len(name) and name[next] == 'A' :
next += 1
min_move = min([min_move, 2 * i + len(name) - next, i + 2 * (len(name)-next)])
# 알파벳 변경(상하이동) 횟수에 좌우 이동 횟수 주가
ans += min_move
return ans
왜 단순히 각 문자 간의 거리를 최소화하는 것이 아니라, 사이에 있는 연속된 'A'의 개수를 고려해야 하는가?
🚀 핵심 개념: A를 지나치는 것이 비효율적일 수 있다!
조이스틱 이동에서 중요한 점은 수정해야 할 문자의 위치에 도달하는 최소한의 이동을 찾는 것이다.
그런데, 단순히 "다음 수정해야 할 문자"까지의 거리만 고려하면 안 되는 이유는 다음과 같다.
"중간에 있는 'A'는 움직이지 않아도 되는 공간이다."
즉, 불필요한 'A'를 지나치는 대신 뒤로 돌아가는 게 더 효율적일 수 있음!
🛠 예제 분석 1: "JAAAN" (연속된 'A'가 있는 경우)
✅ 단순 정방향 이동 (비효율적)
- J를 만들고
- A → A → A 지나가면서 오른쪽으로 이동 (불필요한 이동 발생)
- N을 만들고 종료
➡ 이동 횟수: 4회 (J에서 N까지 3칸 이동)
✅ 효율적인 이동 (뒤로 돌아가기)
- J를 만들고
- 왼쪽으로 이동(◀)하여 N`을 먼저 만든 후
- 다시 J로 돌아옴
➡ 이동 횟수: 2회 (J → N → J)
🚨 결론:
"다음 문자까지의 거리"만 고려하면 불필요한 이동을 할 가능성이 있음!
➡ 연속된 'A'를 피하는 것이 더 적은 이동 횟수를 만들 수도 있다.
🛠 예제 분석 2: "JANAAAAN"
✅ 단순 정방향 이동 (비효율적)
- J → A → N → A → A → A → A → N (7칸 이동)
➡ 이동 횟수: 7회
✅ 효율적인 이동 (뒤로 돌아가기)
- J → A → N 만든 후
- 왼쪽(◀)으로 바로 이동해서 N을 만든다.
- 중간에 AAAA를 건너뛸 수 있음
➡ 이동 횟수: 4회
🚨 결론 : 연속된 'A'가 많을수록, 단순 정방향 이동보다 '우회'가 유리할 수 있다!
🔥 결론: 연속된 'A'가 많을수록 최적 경로가 달라질 수 있다!
단순히 이전 문자와 다음 문자 사이의 거리만 비교하면 불필요한 이동이 발생할 수 있음
A가 연속된 구간을 우회하는 방법을 고려해야 최소 이동이 보장됨! 🚀
1️⃣ 기본적인 좌우 이동 개념
일반적으로, 조이스틱은 오른쪽으로 이동하면서 문자를 변경하는 것이 기본적인 방식이다.
즉, 모든 문자를 방문해야 한다고 가정하면, 기본 이동 횟수는 len(name) - 1 (오른쪽으로 한 칸씩 이동)
min_move = len(name) - 1
하지만, 연속된 'A'가 있는 경우 굳이 오른쪽으로 끝까지 가지 않고 뒤로 돌아가는 것이 유리할 수도 있음
따라서, 연속된 'A'의 위치를 고려하여 최소 이동 횟수를 조정한다.
2️⃣ min_move = min([ ... ]) 식 분석
min_move = min([min_move, 2 * i + len(name) - next, i + 2 * (len(name)-next)])
여기서 i는 현재 검사 중인 문자 위치, next는 연속된 'A' 다음 첫 번째 문자 위치입니다.
각 항목이 의미하는 바를 하나씩 살펴볼게요.
✅ (1) min_move 기본값: len(name) - 1
min_move = len(name) - 1
- 그냥 왼쪽에서 오른쪽으로 끝까지 가는 경우 (가장 단순한 이동 방법)
- "JEROEN"의 경우 "J → E → R → O → E → N"으로 가면 이동 횟수는 5
✅ (2) 2 * i + len(name) - next
2 * i + len(name) - next
🚀 설명:
- i까지 갔다가 다시 되돌아간 후, 반대 방향으로 진행하는 경우
- 즉, 처음 → i까지 진행 → 다시 처음으로 돌아감(index = 0) : i*2 → 뒤쪽 문자로 이동
- "JANAAAAAN" 같은 경우를 고려한 방식
🛠 예제: "JANAAAAAN"
위치 문자
| 0 | J |
| 1 | A |
| 2 | N |
| 3 | A |
| 4 | A |
| 5 | A |
| 6 | A |
| 7 | N |
- 처음부터 J → A → N (i=2)까지 이동
- 다시 되돌아와서 (2*i)
- 'A'가 끝난 후 (next=7 이후)부터 이동
➡ 이동 횟수:
2 * i + len(name) - next = 2 * 2 + 8 - 7 = 4 + 1 = 5
✅ (3) i + 2 * (len(name) - next)
i + 2 * (len(name) - next)
🚀 설명:
- i까지 가고 한 번에 끝까지 가는 대신, 뒤쪽에서 먼저 완성한 후 되돌아오는 경우
- "JANAAAAAN"처럼 뒤쪽에 유효한 문자가 있는 경우 유리할 수 있음
🛠 예제: "JANAAAAAN"
위치 문자
| 0 | J |
| 1 | A |
| 2 | N |
| 3 | A |
| 4 | A |
| 5 | A |
| 6 | A |
| 7 | N |
- J → A → N (i=2)까지 이동
- 곧바로 끝까지 이동 (next=7 이후)
- 다시 N이 있는 곳까지 되돌아옴 (2 * (len(name) - next))
➡ 이동 횟수:
i + 2 * (len(name) - next) = 2 + 2 * (8 - 7) = 2 + 2 = 4
3️⃣ 정리
이동 방법은 총 3가지:
1️⃣ 기본적으로 왼쪽에서 오른쪽으로 이동 (len(name) - 1)
2️⃣ 중간까지 갔다가 다시 처음으로 되돌아오는 경우 (2 * i + len(name) - next)
3️⃣ 끝까지 갔다가 다시 돌아오는 경우 (i + 2 * (len(name) - next))
➡ 세 가지 경우 중 가장 작은 값을 min_move로 업데이트
➡ 결과적으로, 연속된 'A'를 우회하는 최적의 경로를 찾을 수 있음! 🚀
다른 정답 코드 2 : https://sweetburble.tistory.com/226
def solution(name):
count = 0
N = len(name)
for ch in name: # 2. 먼저 커서가 어디있든, A에서 최소로 바꿔야 그 글자가 되는지 모두 계산한다
if (ch != 'A'):
min_up_down = min(ord(ch) - ord('A'), 26 + ord('A') - ord(ch))
count += min_up_down
move = N - 1 # 1. 커서를 좌우로 움직이는 것은, 아무리 최악이어도 문자열을 한번 순회하는 것뿐이다 -> N - 1
for left in range(N):
idx = left + 1
while (idx < N) and (name[idx] == 'A'): # right는 오른쪽 끝에서, left 오른쪽을 기준으로 처음 A가 아닌 알파벳의 위치만큼 빼줘야 한다!
idx += 1
right = N - idx
back_distance = min(left, right) # 한쪽 방향으로 이동 후, 반대 방향으로 이동하는 최소거리를 구한다 -> 그러므로 left나 right 중 최솟값을 한번 더 더하는 것이다.
move = min(move, left + right + back_distance)
count += move
return count