[Python] 백준 1463 1로 만들기
문제 분석
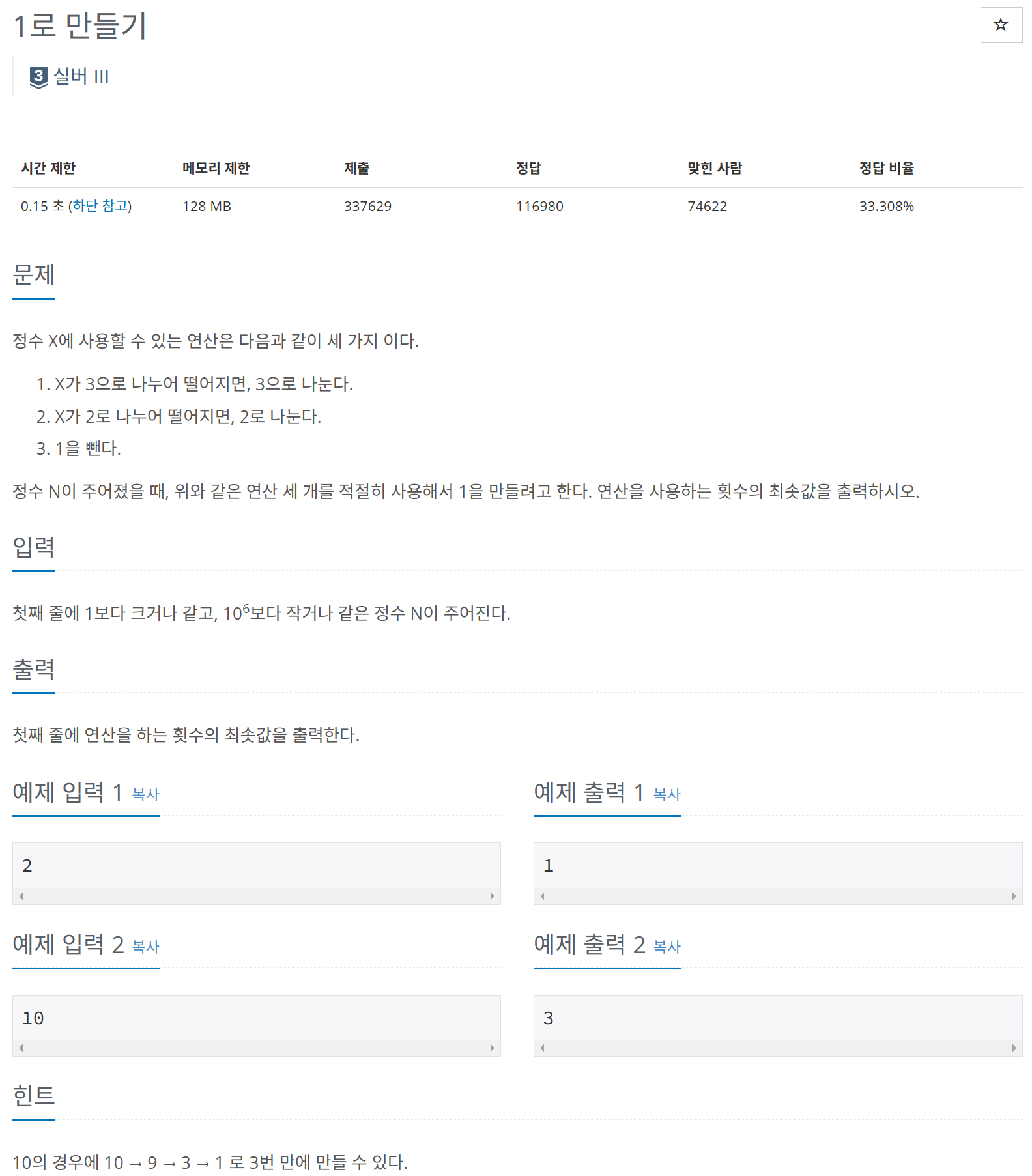
- 3가지 연산을 통해 정수 N을 1로 만들려고 한다.
- 연산을 사용하는 횟수의 최솟값을 출력
코드 설계
- 1차
- 그럼 3으로도 나누어 떨어지고 2로도 나누어 떨어진다면? (6의 배수라면?)
- 더 큰 수인 3으로 나누는게 더 빠르려나? (x)
2차모든 경우의 수를 구하고, 그 중 가장 작은 거를 구해야하나?그러면 어떻게 모든 경우의 수를 구하지?총 3가지의 연산 방법이 있으니까순서o, 중복o 인 중복 순열로 경우의 수를 모두 구하고거기서 각 연산 횟수를 찾고그 중 최소 연산 횟수를 출력(근데 이러면 시간 초과 날거 같은데..)연산 총 횟수 3x3x3 = 81횟수를 모르는데 미리 연산 방법을 어떻게 정함..
정답 코드
1차 - 실패
import sys
input = sys.stdin.readline
n = int(input())
cnt = 0
while True :
if n == 1 :
print(cnt)
break
if n % 6 == 0 :
n = n//3
elif n % 3 == 0 :
n = n // 3
elif n % 2 == 0 :
n = n // 2
else :
n -= 1
cnt += 1
- 이렇게 하면 10의 경우는 최소 횟수인 3이 아니라 4가 출력
- 큰 수로 처음부터 계속 나누는 것이 제일 빨리 1로 도달할 수 있는 방법 -> 그리디
다른 정답 코드 1
- DP
- DP에는 상향식 / 하향식이 있는데 처음 두 수를 알기 때문에 상향식으로 풀이
- 상항식(bottom-up) : 제일 작은 인덱스의 수 부터 목표하는 값까지 향하는 것
- 하향식(top-down) : 맨 위의 값에서 재귀로 가장 작은 인덱스를 향하는 것
- 그리디 vs DP
- 그리디 알고리즘 : 처음 생각한 최적의 방법이 끝까지 반례 없이 적용되는 경우
- DP : 가능성을 모두 두고 그 안에 최솟값 찾기
- 메모이제이션 → 중복 계산되는 값을 저장하여 효율을 높인다.
- 1~N까지 만들어 간다고 할 때 각 숫자에서의 최소 연산 횟수를 저장하면
- 모든 숫자에 대해 호출 할 필요 없이 이전에 계산했던 정보를 그대로 가져다 쓰면 됨
- 즉, dp 테이블에는 해당 숫자를 만드는데 최소 연산 횟수를 저장하게 될 것
- 점화식으로 나타내면
- dp[i] = min(dp[i-1] + 1, dp[i//2] + 1, dp[i//3] +1)
- dp[i//2] +1, dp[i//3] + 1은 2로 나누어 떨어지는 경우와 3으로 나누어 떨어지는 경우에 대해서만 고려해주면 된다.
- 값을 그대로 가져다 쓰기 때문에 시간 복잡도는 O(N)
import sys
input = sys.stdin.readline
n = int(input())
d = [0] * (n+1) # d에 계산된 값 저장
# n+1인 이유는 1번째 수는 d[1]이 아니고 d[2]이기 때문
# 계산하기 편하게 d[1]을 1번째인 것처럼 만듬
# d는 인덱스의 숫자가 1이 되는데 필요한 연산의 최솟값을 갖는다.
# d[1]은 0 : 1이 1로 되는데 필요한 연산은 0회
# d[2]는 2가 1이 되는데 필요한 최소 연산 횟수는 1
# 여기서 왜 if 1빼는 방법, 2 나누기, 3 나누기 동등하게 하지 않고 처음에 1을 빼고 시작하는지 의아해 할 수 있다.
# 1을 빼고 시작하는 이유는 다음에 계산할 나누기가 1을 뺀 값보다 작거나 큼에 따라 어차피 교체되기 때문이다.
# 즉 셋 다 시도하는 방법이 맞다.
# 여기서 if elif else를 사용하면 안된다. if만 이용해야 세 연산을 다 거칠 수 있다.
# 가끔 if continue, else continue를 쓰는 분도 계신데, 난 이게 편한듯.
for i in range(2, n+1) : # 2부터 n까지 반복
d[i] = d[i-1] + 1 # 1을 빼주는 경우는 모든 숫자에 대해서 가능 / 1을 빼는 연산 : 1회 진행
# d[i]는 숫자 i가 1이 되는데 걸리는 최소한의 연산 횟수를 저장해야 합니다.
# i에서 1을 빼면 i-1이 되므로, d[i-1]+1을 함으로써,
# d[i-1] (i-1이 1이 되는데 필요한 최소한의 연산) + 1
# (i에서 1을 빼서 i-1이 되는데 필요한 연산 횟수 1회)로 초기화
if i % 3 == 0 : # 3로 나누어 떨어지는 경우, 최소값 갱신
d[i] = min(d[i], d[i//3] + 1)
# 1을 더하는 것은 d는 결과가 아닌 계산한 횟수를 저장하는 것 이기 때문
# d[i]에는 더하지 않는 이유는 이미 1을 뺄 때 1을 더해준 이력이 있기 때문
if i % 2 == 0 : # 2로 나누어 떨어지는 경우, 최소값 갱신
d[i] = min(d[i], d[i//2] + 1)
print(d[n])
다른 정답 코드 2 - DP (Top-Down, 재귀 사용)
https://bio-info.tistory.com/159
x=int(input())
dp={1:0}
def rec(n):
if n in dp.keys():
return dp[n]
if (n%3==0) and (n%2==0):
dp[n]=min(rec(n//3)+1, rec(n//2)+1)
elif n%3==0:
dp[n]=min(rec(n//3)+1, rec(n-1)+1)
elif n%2==0:
dp[n]=min(rec(n//2)+1, rec(n-1)+1)
else:
dp[n]=rec(n-1)+1
return dp[n]
print(rec(x))dp를 딕셔너리로 초기화합니다. dp가 1일 때, 0 값을 갖는 것의 의미는 1일 때 1이 되는데 필요한 연산 횟수가 0회라는 것입니다. rec함수는 숫자 n을 입력받아, 재귀적으로 dp 딕셔너리를 채워갑니다. rec함수의 종료 조건은 입력받은 n이 dp딕셔너리의 key에 존재하는 경우 dp[n]을 리턴합니다.
if (n%3==0) and (n%2==0):
dp[n]=min(rec(n//3)+1, rec(n//2)+1)
-> n이 3으로도 나누어 떨어지고, 2로도 나누어 떨어지는 경우, rec(n//3)+1, rec(n//2)+1중 최솟값을 dp[n]에 넣습니다. rec(n//3)+1이 의미하는 것은 n을 3으로 나눈 몫이 1이 되는데 필요한 최소 연산 횟수 + n을 3으로 나누는 연산횟수 1회입니다. 즉, 3으로 나눈 경우와 2로 나눈 경우중 연산 횟수가 더 적은 쪽이 dp[n]에 들어갑니다.
elif n%3==0:
dp[n]=min(rec(n//3)+1, rec(n-1)+1)
-> n이 3으로만 나누어 떨어지는 경우는 3으로 나눈 경우(rec(n//3)+1)와 n에서 1을 뺀 뒤, n-1이 1이 되는데 걸리는 최소 연산 횟수인 rec(n-1)+1을 비교하여 최솟값을 dp[n]에 넣습니다.
elif n%2==0:
dp[n]=min(rec(n//2)+1, rec(n-1)+1)
-> n이 2로만 나누어 떨어지는 경우도 마찬가지로 n을 2로 나눈 경우와 n에서 1을 뺀 경우를 비교하여 최솟값을 dp[n]에 넣습니다.
else:
dp[n]=rec(n-1)+1
-> n이 3으로도 나누어 떨어지지 않고, 2로도 나누어 떨어지지 않는 경우는 n에서 1을 뺀 값인 n-1이 1이 되는데 걸리는 최소한의 연산 횟수 + 1회(n에서 1을 빼는 연산 1회)를 dp[n]에 넣어줍니다.
return dp[n]
-> 마지막 return dp[n]은 재귀 호출을 모두 마무리하고, rec(x)의 결과를 최종 반환할 때 쓰입니다.
다른 사람 폴이 3 - BFS
from collections import deque
x=int(input())
Q=deque([x])
visited=[0]*(x+1)
while Q:
c=Q.popleft()
if c==1:
break
if c%3==0 and visited[c//3]==0:
Q.append(c//3)
visited[c//3]=visited[c]+1
if c%2==0 and visited[c//2]==0:
Q.append(c//2)
visited[c//2]=visited[c]+1
if visited[c-1]==0:
Q.append(c-1)
visited[c-1]=visited[c]+1
print(visited[1])BFS 풀이는 Q에 x값을 넣고, x에서 1로 갈 때 최단거리를 찾는 방향입니다. BFS로 탐색한 결과는 항상 최단거리를 보장하기 때문에 이렇게도 풀어보았습니다. 즉, x부터 BFS를 돌며, visited에 방문 표시와 해당 노드에 방문하는데 걸린 횟수를 함께 저장합니다.
예를 들어, x가 10일 때, 2로 나누어 떨어지니까 visited[5]에는 1이 들어갑니다. 10에서 1을 빼면 visited[9]에도 1이 들어갑니다. 그러고 Q에는 각각 5와 9가 들어갑니다. 5일 때는 1을 빼는 연산을 한 번 더 하기 때문에, visited[4]에는 2가 들어갑니다. 9는 3으로 나누어 떨어지니까 visited[3]에도 2가 들어갑니다. 9에서 1뺀 visited[8]에도 2가 들어갑니다. 그러면 현재 Q에는 4,3,8이 들어있습니다. 이중 3에서 3으로 나누어 떨어지니까 바로 1이 되며, visited[1]에는 3이 들어갑니다. 그래서 최종적으로 visited[1]을 출력하면 정답입니다.
2회차 - 25.02.24
다른 정답 코드 1 : https://jominseoo.tistory.com/98
- DP 핵심 아이디어 :
1에서부터 정수 X까지 만들어간다고 할 때, 각 숫자에서의 최소 연산 횟수를 저장해준다면
모든 숫자에 대해 /3, /2, -1 을 하는 함수를 호출할 필요 없이 이전에 계산했던 정보들을 그대로 가져다 쓰면 된다.
import sys
input = sys.stdin.readline
def min_op(n) :
dp = [0] * (n+1) # dp[i] : i를 1로 만들기 위한 최소 연산 횟수
for i in range(2, n+1) :
dp[i] = dp[i-1] + 1 # 1을 빼는 경우
if i % 2 == 0 :
dp[i] = min(dp[i], dp[i//2] + 1) # 2로 나누는 경우
if i % 3 == 0 :
dp[i] = min(dp[i], dp[i//3] + 1) # 3으로 나누는 경우
return dp[n]
n = int(input())
print(min_op(n))1은 항상 수행할 수 있는 연산이기 때문에 1을 빼는 연산을 기본으로 한다.
3회차 - 25.03.27
실패.
import sys
input = sys.stdin.readline
'''
3가지 연산
1. x // 3
2. x // 2
3. x - 1
dp에 저장되는 값은 인덱스에 해당하는 숫자에 대해 최소 연산 횟수
2 -> 1 의 연산 횟수
1) 2 // 2
2) 2 - 1
3 -> 1의 연산 횟수
1) 3 // 3 (v)
2) 3 - 1 = 2의 최소 연산 횟수
'''
x = int(input())
dp = [0 for _ in range(x+1)]
dp[2] = 1
for i in range(3, x+2) :
if (i/3 == 0) and (i/2 == 0) :
dp[i] = min(dp[i//3], dp[i//2], dp[i-1] + 1)
elif (i/3 == 0) and (i/2 != 0) :
dp[i] = min(dp[i//3], dp[i-1])
elif (i/3 != 0) and (i/2 == 0) :
dp[i] = min(dp[i//2], dp[i-1])
else :
dp[i] = dp[i-1]
print(dp[x])
성공
import sys
input = sys.stdin.readline
'''
3가지 연산
1. x // 3
2. x // 2
3. x - 1
dp에 저장되는 값은 인덱스에 해당하는 숫자에 대해 최소 연산 횟수
2 -> 1 의 연산 횟수
1) 2 // 2
2) 2 - 1
3 -> 1의 연산 횟수
1) 3 // 3 (v)
2) 3 - 1 = 2의 최소 연산 횟수
'''
x = int(input())
dp = [0 for _ in range(x+1)]
for i in range(2, x+1) :
dp[i] = dp[i-1] + 1
# i-1에서 1로 가기 위한 최소 연산 횟수 : dp[i-1]
# i-1에서 i로 만들기 위해 연산을 한 번 수행
if i % 2 == 0 :
dp[i] = min(dp[i], dp[i//2] + 1) # -1 이랑 //2 비교
if i % 3 == 0 :
dp[i] = min(dp[i], dp[i//3] + 1)
print(dp[x])