[Python] 프로그래머스 lv.2 더 맵게

알고리즘 고득점 kit - 힙(Heap) - (1)

 

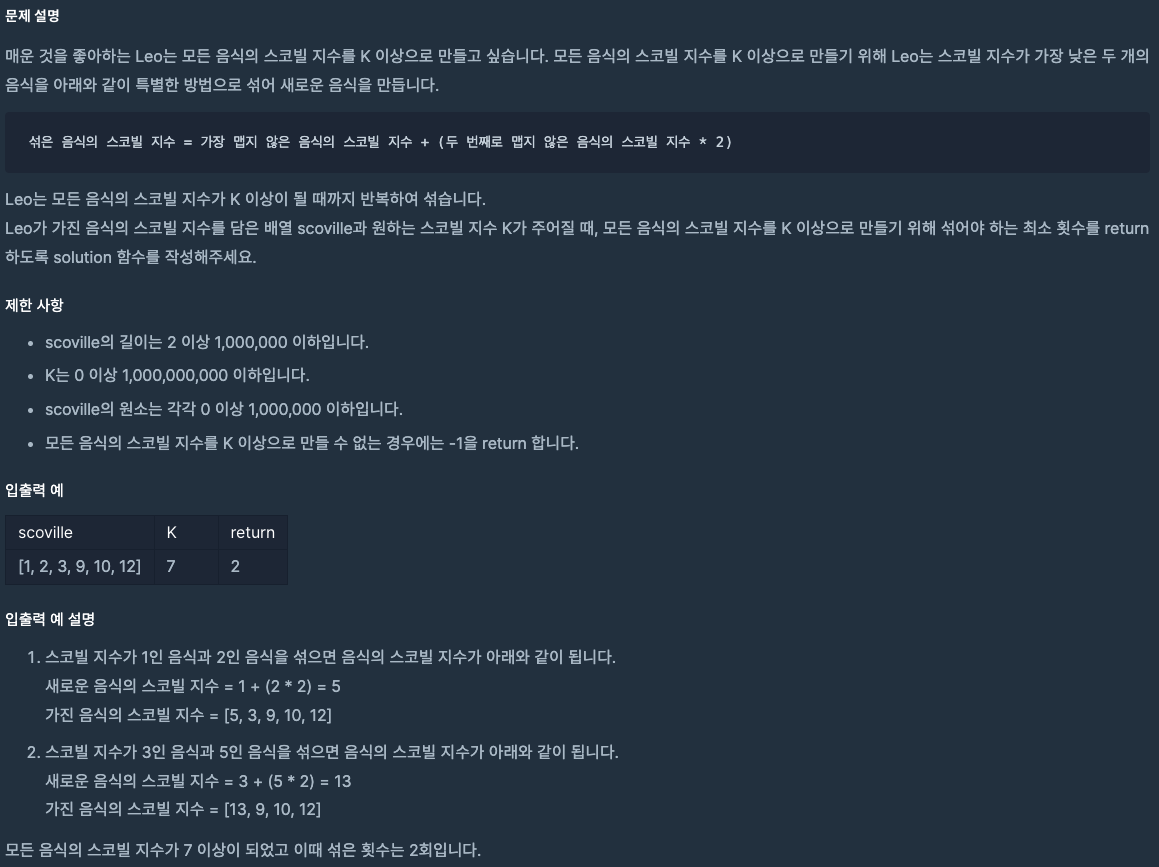
문제 분석

• 모든 음식의 스코빌 지수가 k 이상이 될 때까지 반복해서 섞는데
• 음식을 섞는 방법 : 가장 작은 수 + (두번째로 작은 수 * 2)
• 모든 수가 k 이상이면 음식을 섞은 횟수 return

 

코드 설계

• 음식의 위치는 중요하지 x : 정렬 → 오름차순 : 앞의 두 개 popleft()
• 리스트의 길이가 2 이상이고
• 리스트 안의 값이 모두 k 이상이면 == 리스트의 최솟값이 k 이상이면 ~

• 종료 조건 1 : min(s) >= k

• 모든 음식을 K이상으로 만들 수 없는 경우 : 계산을 했는데 리스트의 길이가 1인 경우
• while 종료조건 2 : len(s) == 1 -> return -1

 

정답 코드

1차 - 실패

from collections import deque

def solution(scoville, K):
    answer = 0
    scoville.sort()
    
    # k 미만의 값만 추출했을 때 빈 값이 아니면 while
    # 빈 값이면 더 이상 스코빌 리스트에 k 미만의 값이 없는 것이므로 break
    while list(s for s in scoville if s > K) : 
        
        sp1 = scoville[0] # 가장 맵지 않은 음식
        sp2 = scoville[1] # 두번째로 맵지 않은 음식
        del scoville[0:2]
        
        scoville.append(sp1 + sp2*2)
        answer += 1
        
    return answer

• 왜 scoville 리스트 길이가 최소 2 이상인데 scoville[1] 에서 인덱스 에러가 나는거지?
• 그리고 모든 음식을 K이상으로 만들 수 없는 경우를 고려하지 않음

 

2차 - 테스트 케이스 : 통과 but 효율성 : 시간초과

def solution(scoville, K):
    answer = 0
    
    while True : 
        scoville.sort()
        
        if min(scoville) >= K : 
            break
            
        if len(scoville) < 2 : 
            return -1
        else : 
            scoville.append(scoville[0] + scoville[1] * 2)
            del scoville[0:2]
            answer += 1
        
    return answer

• while 문을 돌 때마다 정렬을 하는게 시간초과가 나는거 아닐까..
• 값을 넣을 때 바로 최적의 자리를 찾아서 넣..

 

다른 사람 코드 1 - 힙(heap) 큐 알고리즘 구현

• heapq 모듈
  1. heappush(heap, item) : 힙 불변성을 유지하면서 item 값을 heap으로 push
  2. heappop(heap) : 힙 불변성을 유지하면서 heap에서 가장 작은 항목을 pop 하고 반환. 만약 heap이 비어있으면 IndexError 발생
  3. heapify(x) : 리스트 x를 선형 시간으로 제자리에서 힙으로 변환

import heapq

# 최소 힙 생성, push
heap_list = []
heapq.heappush(heap_list, 4)
heapq.heappush(heap_list, 1)
heapq.heappush(heap_list, 7)

# pop
heapq.heappop(heap_list)

# pop하지 않고 최솟값 얻기
print(heap_list[0])

# 기존 리스트를 힙으로 변환
a_list = [4, 1, 7, 3, 8, 5]
heapq.heapify(a_list)

• 힙에서 인덱스 0이 최솟값이라고 해서, 인덱스 1에 두번째, 인덱스 2에 세번째로 작은 원소가 있는 것은 아니다.
• 두번째로 작은 원소를 얻으려면 heappop( )을 통해 최솟값을 삭제한 후 heap[0]으로 접근하거나
• 인덱스 1을 인덱스 2와 비교하는 방법 사용

 

• 스코빌 리스트 → 힙 변환
• 정렬한 리스트의 0번째 값과 1번째 값을 이용하여 섞었을 때 새로운 스코빌 지수 계산
• 이때 0, 1번째 값을 heappop을 이용해 pop
• 계산된 스코빌 지수 heappush를 이용해 push

import heapq

def solution(scoville, K):
    answer = 0
    mix_scoville = 0
    heapq.heapify(scoville)         # 최초 리스트에서 힙 정렬
    
    while scoville[0] < K:          # 스코빌이 기준점 넘어가면 반복 종료
        if(len(scoville)<2):        # 스코빌 지수 하나 남았을 때 더 이상 불가하므로 -1 리턴
            return -1
        mix_scoville = heapq.heappop(scoville) + (heapq.heappop(scoville)*2)
        heapq.heappush(scoville,mix_scoville)           
        answer +=1                          
       # 그 외에는 스코빌 계산하면서 값 빼주고 나온값 push
        
    return answer

 

다른 사람 코드 2

import heapq

def solution(ss, K) : 
    ans = 0
    heapq.heapify(ss)
    
    while ss[0] < K : 
        mix = heapq.heappop(ss) + heapq.heappop(ss) * 2
        heapq.heappush(mix)
        ans += 1
        
        if len(ss) == 1 and ss[0] < K : 
            return -1
    
    return ans

 

 

2회차 - 25.02.12

import heapq

def solution(scoville, K): # 최소 스코빌 값 : K
    answer = 0
    heapq.heapify(scoville)
    
    while(scoville) :
        if len(scoville) >= 2 : 
            min1 = heapq.heappop(scoville)
            min2 = heapq.heappop(scoville)
            if min(min1, min2) >= K : # 가장 작은 값이 K이상이면 끝
                break
            answer += 1
            heapq.heappush(scoville, min1 + (min2*2))
        else : 
            if sum(scoville) >= K :
                break
            else : 
                answer = -1
                break
    return answer

 

다른 정답 코드 1

import heapq as hq

def solution(scoville, K):

    hq.heapify(scoville)
    answer = 0
    while True:
        first = hq.heappop(scoville)
        if first >= K:
            break
        if len(scoville) == 0:
            return -1
        second = hq.heappop(scoville)
        hq.heappush(scoville, first + second*2)
        answer += 1  

    return answer